Bronisław Knaster (Warszawa), Sur un continu que tout sous-continu divise

1. Introduction. On dit qu’un ensemble $B$ divise un ensemble connexe $A$ , quand l’ensemble $A - B$ n’est pas connexe (Un ensemble $E$ est dit connexe (au sens de Lennes–Hausdorﬀ), lorsque les formules $E = M + N$ , $M \neq O \neq N$ entraînent $\bar{M} N + M \bar{N} \neq 0$ , le symbole $\bar{X}$ désignant d’une façon générale la somme de l’ensemble $X$ et de celui de ses points-limites.).

Les problèmes concernant la division des continus par leurs sous-continus ne sont résolus jusqu’à présent qu’en partie. On sait qu’il existe des continus qu’aucuu sous-continu ne divise: tels sont, par exemple, les courbes simples fermées et les continus indécomposables. On peut montrer également que

\begin{matrix} \begin{aligned} tout continu de Jordan renferme \\ un sous-continu qui ne le divise pas. \end{aligned} \end{matrix}

(1)

Soient, en eﬀet, $B$ un sous-continu divisant un continu jordanien $A$ et $C$ une composante (= „Komponente” au sens de Hausdorﬀ, c’est-à-dire, tout sous-ensemble connexe qui ne peut être augmenté sans cesser d’être sous-ensemble connexe.) arbitraire de $A - B$ . Par conséquent, $A - C$ ne divise pas $A$ . Or, $A - C$ est un continu, car $C$ étant un ensemble ouvert dans $A$ (C. Kuratowski, Une déﬁnition topologique de la ligne de Jordan, Fund. Math. I, p. 43, th. (6).), l’ensemble $A - C$ est fermé; d’autre part il est connexe en vertu d’un théorème général (B. Knaster et C. Kuratowski, Sur les ensembles connexes, Fund. Math. II, p. 214, th. X.).

Le problème s’impose donc s’il en est de-même de tous les continus, quels qu’ils soient (Ce problème fut posé par M. Zarankiewicz et moi en 1926, Fund. Math. VIII, p. 376, probl. 42.). Je vais donner ici la solution négative de ce problème, en déﬁnissant (dans l’espace euclidien à 3 dimensions) un continu borné $A$ et démontrant la propriété (P) suivante de ce continu:

\begin{matrix} \begin{aligned} B étant un vrai sous continu arbitraire \\ de A qui ne se réduit pas à un point, \\ l’ensemble A - B n’est pas connexe. \end{aligned} \end{matrix}

(P)

Bien entendu, un tel continu $A$ est en raison de (1) nonjordanien.

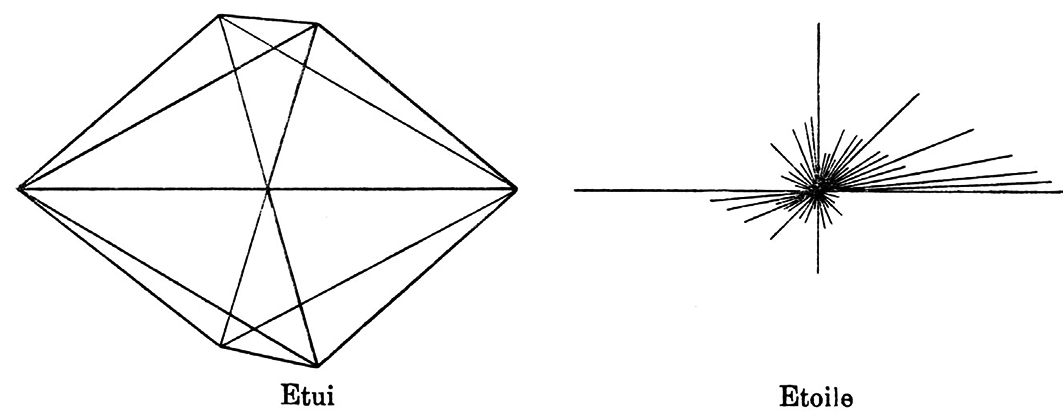
2. Figures auxiliaires. Soient: $D$ un segment rectiligne à extrémités $a (D)$ et $b (D)$ , $c (d)$ son point médian, $T (D)$ un triangle isocèle à sommet $c (D)$ situé dans un plan perpendiculaire à $D$ , $H (D)$ la hauteur de $T (D)$ , $E (D)$ la somme de deux pyramides ayant $T (D)$ pour base commune et pour sommets respectivement les extrémités de $D$ . Soit enﬁn $E^{'} (D)$ le polyèdre symétrique à $E (D)$ selon $D$ comme axe de symétrie.

J’appelle étui de $D$ l’ensemble

F (D) = E (D) + E^{'} (D) .

Cet ensemble est la première approximation du continu $A$ à construire. Quel que soit $D$ , convenons une fois pour toutes de prendre $δ H (D) \leq \frac{δ (D)}{2}$ , de façon à avoir

δ F (D) = δ (D) .

(2)

Soient $R_{0} (D)$ le rhombe formant l’intersection de $F (D)$ avec le plan $P (D)$ qui passe par $D + H (D)$ et $R_{m} (D)$ où $m = 1, 2, \dots$ le rhombe contenu dans $R_{0} (D)$ , concentrique avec lui et ayant les cotés parallèles aux siens, mais $2^{m}$ fois plus courts. Considérons l’inﬁnité dénombrable de segments déﬁnis comme parties communes des $R_{m} (D)$ avec les rayons inﬁnis (demi-droites) situés sur $P (D)$ , issus de $c (D)$ et faisant avec le rayon $\vec{c (D), b (D)}$ les angles:

\begin{array}{l} π & (\frac{1}{2^{i_{1}}} + \frac{1}{2^{i_{1} + i_{2}}} + \dots + \frac{1}{2^{i_{1} + i_{2} + \dots + i_{j}}} \\ + \dots + \frac{1}{2^{i_{1} + i_{2} + \dots + i_{j} + \dots + i_{m}}}) \end{array}

où

i_{j} = 0, 1, 2, \dots ad inf. et j = 1, 2, \dots, m .

Rangeons tous ces segments en suite inﬁnie

D_{1}^{1}, L_{2}^{1}, \dots, D_{k}^{1}, \dots k = 1, 2, \dots

(3)

où $D_{1}^{1}$ et $D_{2}^{1}$ en désignent respectivement les plus grands, à savoir les deux moitiés de $D$ à extrémités libres $a (D)$ et $b (D)$ et posons:

G (D) = \sum_{k = 1}^{\infty} D_{k}^{1} .

(4)

J’appelle étoile de centre $c (D)$ le continu $G (D)$ ainsi déﬁni.

Si l’on ordonne tous les segments $D_{k}^{1}$ selon leurs angles décroissants avec $D$ , ils forment un type d’ordre dense; cependant, ceux d’entre eux qui sont déterminés par un $R_{m} (D)$ donné constituent une suite transﬁnie du type $ω^{m + 1}$ . Comme le point $c (D)$ divise $G (D)$ , on en déduit facilement que

\begin{matrix} \begin{aligned} G (D) & - c (D) est formé d’une inﬁnité dènombrable \\ de composantes D_{k}^{1} - c (D), dont chacune est, \\ dans sa moitié contigue à c (D), composée de \\ points-limites des autres (D_{2}^{1} l’est d’ailleurs \\ entièrement) . \end{aligned} \end{matrix}

(5)

En désignant respectivement par $a (D_{k}^{1}) = c (D)$ , $b (D_{k}^{1})$ et $c (D_{k}^{1})$ les extrémités et le point médian de $D_{k}^{1}$ , on a donc d’après (5):

c (D_{k}^{1}) \subset \bar{G (D) - D_{k}^{1}} .

(6)

L’autre propriété essentielle de l’étoile est sa situation dans $F (D)$ qui permet, comme on peut le vériﬁer géométriquement, d’entourer chacun de ses segments $D_{k}^{1}$ d’un étui $F (D_{k}^{1})$ , analogue à $F (D)$ , de manière que les conditions suivantes soient remplies:

\begin{align} F (D_{k}^{1}) & \subset F (D) & (7) \\ F (D_{k}^{1}) & . \sum_{h \neq k} F (D_{h}^{1}) = D_{k}^{1} . \sum_{h \neq k} D_{h}^{1} = c (D) & (8) \\ lim_{j \to \infty} F (D_{k_{j}}^{1}) & = lim_{j \to \infty} D_{k}^{1}, pour toute suite de segments (3). & (9) \end{align}

Il suﬃt à ce but de former d’abord les étuis $F (D_{1}^{1})$ et $F (D_{2}^{1})$ , conformes à (2) où $E (D_{t}^{1}) \subset E (D)$ , $E^{'} (D_{t}^{1}) \subset E^{'} (D)$ et $E (D_{t}^{1}) . P (D) = D_{t}^{1}$ $(t = 1, 2)$ , pour pouvoir ensuite entourer d’accord avec (7) tous les autres segments $D_{k}^{1}$ des étuis à $δ H (D_{t}^{1})$ décroissant assez rapidement pour que les conditions (8) et (9) soient aussi réalisées. Contrairement aux deux premiers étuis, les autres se trouveront nécessairement situés en entier soit dans $E (D)$ , soit dans $E^{'} (D)$ .

$G (D)$ étant un continu, l’ensemble $\sum_{k = 1}^{\infty} F (D_{k}^{1})$ l’est également en vertu de (9). Il formera la seconde approximation du continu $A$ .

3. Déﬁnition de l’exemple A. Etant donnés d’une façon générale une ﬁgure quelconque $I$ formée de segments rectilignes ayant deux à deux tout au plus une extrémité commune, $F (I)$ la somme de leurs étuis assujettis aux conditions (7)–(9) et $G (I)$ la somme des étoiles construites dans $F (I)$ sur les segments de $I$ , soient:

G_{0} = D, \dots, F_{n} = F (G_{n}), G_{n} = G (G_{n - 1}), \dots

(10)

Il résulte par induction des déﬁnitions des fonctions $F$ et $G$ que de tels $F_{n}$ et $G_{n}$ existent pour tout $n = 0, 1, 2, \dots$ , que la suite ${F_{n}}$ est décroissante, la suite ${G_{n}}$ croissante et que l’on a $G_{n} \subset F_{n}$ . Posons:

A = \prod_{n = 0}^{\infty} F_{n},

(11)

où, ce qui revient au même en vertu de (2), (7) et (9),

A = \bar{\sum_{n = 0}^{\infty} G_{n}} .

(12)

4. Propriétés de l’exemple A. Ainsi déﬁni, $A$ est donc un continu. Considérons un segment arbitraire $D_{k}^{n}$ de $G_{n}$ où $n \geq 1$ et désignons

1^*: par $D_{k}^{n - 1}$ celui des segments de $G_{n - 1}$ dont l’étoile $G (D_{k}^{n - 1})$ contient $D_{k}^{n}$ .
2^*: par $D_{l_{1}}^{n + 1}, D_{l_{2}}^{n + 1}, \dots, D_{s}^{n + 1}, \dots$ la suite de segments de $G_{n + 1}$ , dont se compose l’étoile $G (D_{k}^{n})$ .

En vertu de (8),

\begin{matrix} \begin{aligned} c (D_{k}^{n}) divise A entre tous deux points dont l’un est \\ situé dans F (D_{l_{s}}^{n + 1}) et l’autre en dehors de cet étui. \end{aligned} \end{matrix}

(13)

(c’est-à-dire que ces points appartiennent à deux composantes diﬀérentes de $A - c (D_{k}^{n})$ .)

Je vais en déduire que

\begin{matrix} \begin{aligned} pour tout vrai sous-continu B de A ne se réduisant pas \\ à un point il existe un n et un k tels que c (D_{k}^{n}) \subset B . \end{aligned} \end{matrix}

(14)

Soit, en eﬀet, $C$ l’ensemble des centres des étoiles de $A$ . Il s’agit de montrer que $B C \neq 0$ .

$C$ étant dénombrable, considérons deux points $p$ et $q$ de $B - C$ . Le diamètre maximal des segments de $G_{n}$ et par conséquent celui de leurs étuis tendant d’après (2) à $0$ avec $n$ croissant, il existe un $n$ tel que

ρ (p, q) > m a x δ F (D_{l_{s}}^{n + 1}) .

(15)

Comme par déﬁnition de $F_{n}$ on a pour tout $n$ : $A = \sum_{k = 1}^{\infty} A . F (D_{k}^{n})$ ( $A$ est même homéomorphe, sinon semblable, à tout sommande de cette somme) et $A . F (D_{k}^{n}) \subset \sum_{s = 1}^{\infty} A . F (D_{l_{s}}^{n + 1})$ , il existe un $k$ et un $l$ , tels que $p \subset A$ . $F (D_{l_{s}}^{n + 1})$ , d’où en vertu de (15): $q \subset A - F (D_{l_{s}}^{n + 1})$ . Les deux dernières inclusions impliquent selon (13) que $c (D_{k}^{n})$ , qui est distinct de $p$ et $q$ , divise $A$ entre ces points; il appartient donc nécessairement au continu $B$ qui les unit.

La propriété (14) étant ainsi démontrée, on en conclut immédiatement que l’ensemble

C = \sum_{n = 0}^{\infty} \sum_{k = 1}^{\infty} c (D_{k}^{n})

(16)

est dense dans $A$ . En formule:

\bar{C} = A .

(17)

Ceci établi, je passe à la démonstration de la propriété (P) de l’exemple $A$ . Supposons donc à présent qu’un sous-continu $B$ ne divise pas $A$ . Il s’agit de prouver que l’on aura alors $B = A$ , ce qui se réduit en vertu de (17) à montrer que

C \subset B .

(18)

si c (D_{k}^{n}) \subset B, on a \sum_{s = 1}^{\infty} c (D_{l_{s}}^{n + 1}) \subset B .

(19)

En eﬀet, le point $c (D_{k}^{n})$ et, à plus forte raison, son sur-ensemble $B$ divise $A$ d’après (13) entre tous deux points de $G (D_{k}^{n}) - B$ situés sur des segments diﬀérents de l’étoile $G (D_{k}^{n})$ . Il existe donc tout au plus un seul $l$ , tel que $D_{l_{s}}^{n + 1} - B \neq 0$ . On a par conséquent $G (D_{k}^{n}) - D_{l_{s}}^{n + 1}$ , d’où $\bar{G (D_{k}^{n}) - D_{l_{s}}^{n + 1}} \subset B$ . Il en résulte d’une part que $c (D_{l_{s}}^{n + 1}) \subset B$ pour tout $t \neq s$ et d’autre part, en vertu de la propriété (6) de la fonction $G$ , que $c (D_{l_{s}}^{n + 1}) \subset B$ .. La démonstration de (19) s’achève par l’addition des deux dernières inclusions.

En appliquant (19) par induction aux points $c (D_{l_{s}}^{n + 1})$ et ainsi de suite, on en déduit que $C . G (D_{k}^{n}) \subset B$ . Comme $C$ est d’après (14) dense dans tout sous-continu de $A$ , donc en particulier dans $G (D_{k}^{n})$ , on a $G (D_{k}^{n}) \subset B$ , et comme $c (D_{k}^{n - 1}) = a (D_{k}^{n}) \subset D_{k}^{n} \subset G (D_{k}^{n})$ on conclut que

si c (D_{k}^{n}) \subset B, on a c (D_{k}^{n - 1}) \subset B .

(20)

En appliquant (20) de proche en proche, on arrive à l’inclusion $c (D^{0}) = c (D) \subset B$ , d’où on conclut, en appliquant (19) par induction suivant la formule (16), que $C \subset B$ , c. q. f. d.

Il est à remarquer que la question si un continu $A$ à propriété (P) existe sur le plan reste ouverte.